evaluates polynomial value 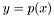 .
.
Evaluates 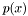 by Horner's recurence. This is the preferred way of evaluating polynomials, since the member function Polynomial<T>::eval() is resricted to same-type polynomial coeficients and variable x
by Horner's recurence. This is the preferred way of evaluating polynomials, since the member function Polynomial<T>::eval() is resricted to same-type polynomial coeficients and variable x
No error checking is performed, so any validation for overflow, or underflow is the responsibility of the caller.
- Parameters:
-
[in] p a polynomial. [in] x parameter of 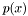
[out] e round-off error to be expected in the calculation of 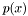
- Returns:
- The value of
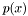 .
.
Definition at line 896 of file Polynomial.h.
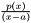 .
.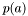 and polynomial
and polynomial 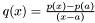 at the same time by Horner's recurence.
at the same time by Horner's recurence.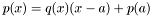 , which essentially means that
, which essentially means that 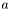 is a root of
is a root of 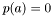 ), this operation is called deflation. That is, on exit
), this operation is called deflation. That is, on exit 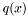 will have all the roots of
will have all the roots of 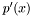 , and second derivative
, and second derivative 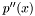 at the same time.
at the same time.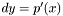 at the same time.
at the same time.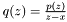
 1.4.5
1.4.5