returns the Cauchy lower bound for a polynomial.
approximates the Cauchy lower bound for polynomial p.
This function expects the input polynomial to be of the form:
![\[p(x)=-|a_0|+|a_1|x+|a_2|x^2+...+|a_n|x^n\]](form_46.png)
where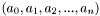 
are real or complex coeficients of the polynomial being examined. The Cauchy lower bound is the value of the only positive zero of 
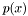. This zero is found using Newton-Raphson method.
The optional parameter upperBound indicates a starting point from where to start looking for this zero. If upperBound is omited, or null, the geometric mean of the zeros will be used as a starting point for the search.
- Example:
#include <complex> #include "polynomial.h" #include "polyzero.h" void main() { // this example shows how to compute the Cauchy lower bound // of a polynomial Polynomial< std::complex<double> > p; Polynomial<double> mp; // initialize polynomial p ... // compute Cauchy polynomial modulus(p, mp) mp[0] = -mp[0]; // compute Cauchy lower bound of polynomial p double c = cauchyLowerBound(mp, 0); // do something ... }
- Parameters:
-
[in] p polynomial being evaluated. Template parameter T can be any non-complex IEEE floating-point type. [in] upperBound starting point to use for the search.
- Returns:
- The Cauchy lower bound.
- See also:
- Polynomial
newtonZero()
Definition at line 233 of file polyzero.h.
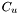is the result of the equation![\[C_u=1+max_n(|a_0|,|a_1|,...,|a_n|)\]](form_49.png)
![\[p(x)=a_0+a_1{x}+a_2{x^2}+...+a_n{x^n}\]](form_33.png)
![\[q(x)=|a_0|+|a_1|{x}+|a_2|{x^2}+...+|a_n|{x^n}\]](form_34.png)
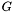for the zeros of a polynomial can be simplified to the result of the equation:![\[G_p=\left[\frac{|a_0|}{|a_n|}\right]^{\frac{1}{n}}, p(x)=a_0+a_1{x}+a_2{x^2}+...+a_n{x^n}, a_n\neq 0\]](form_51.png)
