Polynomial< T > Class Template Reference
[The Polynomial Templates]

#include <Polynomial.h>

Inheritance diagram for Polynomial< T >:

List of all members.

Detailed Description

template<class T>
class Polynomial< T >

defines operations on polynomials.

Class Polynomial is based on the class std::vector, and thus requires the Standard C++ Library (STL).

Coeficients are stored with lowest degree coeficent first, i.e.: the polynomial 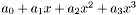${a_0}+{a_1}x+{a_2}x^2+{a_3}x^3$ will be stored in the vector as $[a_0, a_1, a_2, a_3]$ .

The coeficient 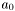$a_0$ of degree 0 is always populated. That means P[0] will always be valid for a polynomial P.

Evaluations are made using Horner's recurence, or synthetic division.

Valid types for template parameter T are any floating point, or complex types which define operators +, -, *, /, and functions abs().

Several constructors are available, the following example shows them and their usage.

Example:
// constructor.cpp : show usage of Polynomial class constructors.
#include <vector>
#include <polynomial.h>

int main() {

    // Initialize p(x) = 5x^4 + 3x^2 + x + 10
    Polynomial<double> p(4, 10., 1., 3., 0., 5.);

    // Initialize q(x) = x^3 + x^2 - 5x + 2
    Polynomial<double> q(3, 2., -5., 1., 1.);

    // Initialize r(x) = x^20 - 1
    Polynomial<double> r;
    r.resize(21);
    r[20] = 1;
    r[0] = -1;

    // initialize u(x) = 1
    Polynomial<double> u(1.);

    std::vector<float> v;
    Polynomial<float> t;

    // initialize v
    //...

    // create a polynomial from vector v
    t = v;

    return 0;
}
Author:
Michael Roy tika1966@yahoo.com
Version:
0.1
See also:
polynomial.h for general support function
polyzero.h for polynomial roots support funtions
laguerre.h for roots-finding by Laguerre's method
muller.h for roots-finding by Muller's method

Definition at line 86 of file Polynomial.h.

Public Member Functions

Construction
 Polynomial (const T &a=T(0))
 Polynomial (const std::vector< T > &p)
 Polynomial (unsigned n, T a0,...)
Methods
void compact ()
int degree () const
int degree ()
void shift (int n)
void makeMonic ()
bool isMonic () const
void getDerivative (Polynomial< T > &pp) const
Evaluation
T eval (const T &x) const
T evalAndDeflate (const T &a, Polynomial< T > &q) const
T evalAndDerive (const T &x, T &ppx) const
Operators
const Polynomial< T > & operator= (const std::vector< T > &q)
const Polynomial< T > & operator+= (const Polynomial< T > &q)
const Polynomial< T > & operator-= (const Polynomial< T > &q)
const Polynomial< T > operator *= (const Polynomial< T > &p)
const Polynomial< T > & operator *= (const T &f)
Polynomial< T > & operator/= (const T &s)

Friends

Non-member operators
Polynomial< T > operator+ (const Polynomial< T > &p, const Polynomial< T > &q)
Polynomial< T > operator- (const Polynomial< T > &p, const Polynomial< T > &q)
Polynomial< T > operator * (const Polynomial< T > &p, const Polynomial< T > &q)
Polynomial< T > operator * (const T &s, const Polynomial< T > &p)
Polynomial< T > operator/ (const Polynomial< T > &p, const T &s)

Constructor & Destructor Documentation

template<class T>
Polynomial< T >::Polynomial (  const T &  a = T(0)  )  [inline, explicit]
 

default constructor.

Creates an empty polynomial of degree zero, you can optionally specify a scalar value.

Parameters:
[in] a default scalar value for coeficient $a_0$ .

Definition at line 100 of file Polynomial.h.

template<class T>
Polynomial< T >::Polynomial (  const std::vector< T > &  p  )  [inline, explicit]
 

copy constructor.

Creates an exact copy of Polynomial $p$

Parameters:
[in] p source polynomial.

Definition at line 113 of file Polynomial.h.

template<class T>
Polynomial< T >::Polynomial (  unsigned  n,
T  a0,
  ...
)  [inline]
 

initialization constructor.

Initializes a polynomial of arbitrary size and coeficients. Care must be taken to properly cast the variable arguments to the same type as template type T.

Parameters:
[in] n polynomial's degree
[in] a0 degree 0 coeficient
[in] ... coeficients $a_1..a_n$ , number of parameters must match parameter n.

Definition at line 127 of file Polynomial.h.

Member Function Documentation

template<class T>
void Polynomial< T >::compact (   )  [inline]
 

compacts array.

Compacts array size to match actual polynomial degree by enforcing the rule p[p.size() - 1] != 0.

This function is called by other member functions to enforce the rule automatically whenever operations are performed on the polynomial.

See also:
degree()

Definition at line 168 of file Polynomial.h.

template<class T>
int Polynomial< T >::degree (   )  [inline]
 

returns degree of polynomial.

Degree of the polynomial is the index of the highest degree non_null coeficient.

This non-constant version of the function calls compact() before returning.

Returns:
The degree of the polynomial.
See also:
degree() const

Definition at line 208 of file Polynomial.h.

template<class T>
int Polynomial< T >::degree (   )  const [inline]
 

returns degree of polynomial.

Degree of the polynomial is the index of the highest degree non_null coeficient.

Example:
// degree.cpp : Shows use of degree()
//
#include <iostream>
#include <polynomial.h>

using namespace std;

int main() {

    // Initialize p(x) = 5x^4 + 3x^2 + x + 10
    Polynomial<double> p(4, 10., 1., 3., 0., 5.);

    // Initialize q(x) = x^3 + x^2 - 5x + 2
    Polynomial<double> q(3, 2., -5., 1., 1.);

    //  Add p and q
    Polynomial<double> r = p + r;

    //  Display degree of new polynomial
    cout << "degree of r(x): " << r.degree() << endl;

    return 0;
}
Program output:
degree of r(x): 4
Returns:
the degree of the polynomial.
See also:
degree()

Definition at line 188 of file Polynomial.h.

template<class T>
T Polynomial< T >::eval (  const T &  x  )  const [inline]
 

evaluates polynomial value $p(x)$ .

Evaluates $p(x)$ by Horner's recurence.

No error checking is performed, so any validation for overflow, or underflow is the responsibility of the caller.

Parameters:
[in] x parameter of $p(x)$
Returns:
The value of $p(x)$ .

Definition at line 312 of file Polynomial.h.

template<class T>
T Polynomial< T >::evalAndDeflate (  const T &  a,
Polynomial< T > &  q
)  const [inline]
 

evaluates polynomial value p(a), and computes $\frac{p(x)}{(x - a)}$ .

Evaluates $p(a)$ and polynomial $q(x)=\frac{p(x)-p(a)}{(x - a)}$ at the same time by Horner's recurence.

It can be shown that $p(x)=q(x)(x - a)+p(a)$ , which essentially means that $p(a)$ is the remainder of $\frac{p(x)}{(x - a)}$ . For the special case where $a$ is a root of $p(x)$ (i.e. $p(a)=0$ ), this operation is called deflation. That is, on exit $q(x)$ will have all the roots of $p(x)$ , except for the root $a$ .

No error checking is performed, so any validation for overflow, or underflow is the responsibility of the caller.

Parameters:
[in] a parameter of $p(a)$ .
[out] q on exit contains the quotient $q(x)=\frac{p(x)-p(a)}{(x - a)}$ .
Returns:
$p(a)$ , the remainder of $\frac{p(x)}{(x - a)}$ .
See also:
evalAndDeflate(const Polynomial<T>& p, const U& x, Polynomial<U>& q, V& e)

Definition at line 339 of file Polynomial.h.

template<class T>
T Polynomial< T >::evalAndDerive (  const T &  x,
T &  ppx
)  const [inline]
 

evaluates $p(x)$ and derivate $dy=p'(x)$ at the same time.

Evaluates efficiently $p(x)$ and first derivative $p'(x)$ at the same time.

Parameters:
[in] x variable to evaluate.
[out] ppx on exit contains $p'(x)$ .
Returns:
The value of $p(x)$ .

Definition at line 354 of file Polynomial.h.

template<class T>
void Polynomial< T >::getDerivative (  Polynomial< T > &  pp  )  const [inline]
 

get derivative of $p(x)$ .

Computes the first derivative polynomial $p'(x)$ of polynomial $p(x)$ .

Parameters:
[out] pp on exit, contains the first derivative $p'(x)$ .
See also:
evalAndDerive(const T& x, T& ppx) const

Definition at line 287 of file Polynomial.h.

template<class T>
bool Polynomial< T >::isMonic (   )  const [inline]
 

indicates if polynomial is monic. Indicates if polynomial is monic. A polynomial is said monic if its highest degree coeficient equals 1.

Returns:
true if polynomial is monic.
See also:
makeMonic()

Definition at line 273 of file Polynomial.h.

template<class T>
void Polynomial< T >::makeMonic (   )  [inline]
 

makes polynomial monic.

Makes polynomial monic. A polynomial is said monic if its highest degree coeficient equals 1.

See also:
isMonic() const

Definition at line 257 of file Polynomial.h.

template<class T>
const Polynomial<T>& Polynomial< T >::operator *= (  const T &  f  )  [inline]
 

in-place polynomial scaling.

Polynomial scaling, performs the operation $p(x)\leftarrow s.p(x)$ .

Returns:
A constant reference to this.
See also:
mul(Polynomial<T>& r, const T& s, const Polynomial<T>& p)
Polynomial<T>::operator*= (const T& f)
operator/ (const T& f, const Polynomial<T>& p)

Definition at line 451 of file Polynomial.h.

template<class T>
const Polynomial<T> Polynomial< T >::operator *= (  const Polynomial< T > &  p  )  [inline]
 

in-place polynomial multiply.

Multiplies two polynomials by convolution. Performs the operation $p\leftarrow pq$

Parameters:
[in] p a polynomial to multiply to this object.
Returns:
A const reference to this.
See also:
mul(Polynomial<T> & r, const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial::operator* (const Polynomial<T>& p, const Polynomial<T>& q)

Definition at line 433 of file Polynomial.h.

template<class T>
const Polynomial<T>& Polynomial< T >::operator+= (  const Polynomial< T > &  q  )  [inline]
 

in-place polynomial addition.

Performs the addition $r=p+q$ , storing the result stored in this.

Parameters:
[in] q a polynomial.
Returns:
A const reference to this.
See also:
operator+ (const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial::operator-= (const Polynomial<T>& A)
add(Polynomial<T>& p, const Polynomial<T>& q)

Definition at line 397 of file Polynomial.h.

template<class T>
const Polynomial<T>& Polynomial< T >::operator-= (  const Polynomial< T > &  q  )  [inline]
 

in-place polynomial substraction. Performs the substraction $r=p-q$ and stores the resulting polynomial in this.

Parameters:
[in] q a polynomial.
Returns:
A const reference to this.
See also:
operator- (const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial::operator+= (const Polynomial<T>& A)
sub(Polynomial<T>& p, const Polynomial<T>& q)

Definition at line 415 of file Polynomial.h.

template<class T>
Polynomial<T>& Polynomial< T >::operator/= (  const T &  s  )  [inline]
 

in-place polynomial scaling.

Polynomial scaling, performs the operation $p(x)\leftarrow \frac{p(x)}{s}$ .

Returns:
A constant reference to this.
See also:
mul(Polynomial<T>& r, const T& s, const Polynomial<T>& p)
Polynomial<T>::operator*= (const T& s)
operator/ (const Polynomial<T>& p, const T& s)

Definition at line 468 of file Polynomial.h.

template<class T>
const Polynomial<T>& Polynomial< T >::operator= (  const std::vector< T > &  q  )  [inline]
 

make a copy of a polynomial.

Make a copy of a polynomial.

Parameters:
[in] q polynomial to copy.
Returns:
A const reference on this object.

Definition at line 379 of file Polynomial.h.

template<class T>
void Polynomial< T >::shift (  int  n  )  [inline]
 

shifts the coeficients.

Shifts the polynomial coeficients left or right, effectively doing the operation $q(x)=x^{n}p(x)$ .

If n is negative, the remainder of the division $\frac{p(x)}{x^{-n}}$ is lost.

Parameters:
[in] n power of multipler $x^n$ .

Definition at line 230 of file Polynomial.h.

Friends And Related Function Documentation

template<class T>
Polynomial<T> operator * (  const T &  s,
const Polynomial< T > &  p
)  [friend]
 

out-of_place polynomial scaling.

Polynomial scaling.

Returns:
The polynomial $r(x)=s.p(x)$ .
See also:
mul(Polynomial<T>& r, const T& s, const Polynomial<T>& p)
Polynomial<T>::operator*= (const T& s)
operator/ (const T& s, const Polynomial<T>& p)

Definition at line 548 of file Polynomial.h.

template<class T>
Polynomial<T> operator * (  const Polynomial< T > &  p,
const Polynomial< T > &  q
)  [friend]
 

out-of-place polynomial multiply.

Multiplies two polynomials by convolution. It is advisable to use mul() instead, as it avoids the copying of the resulting polynomial off the stack.

Parameters:
[in] p a polynomial.
[in] q another polynomial.
Returns:
The product $r=pq$
See also:
mul(Polynomial<T> & r, const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial::operator*= (const Polynomial<T>& p)

Definition at line 530 of file Polynomial.h.

template<class T>
Polynomial<T> operator+ (  const Polynomial< T > &  p,
const Polynomial< T > &  q
)  [friend]
 

out-of-place polynomial addition.

Performs the addition $r=p+q$ .

Calling directly the three parameters function add() is actually more efficient, as it will avoid an unnecessary copy of the polynomial.

See also:
operator- (const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial<T>::operator+= (const Polynomial<T>& p)
add(Polynomial<T>& r, const Polynomial<T>& p, const Polynomial<T>& q)

Definition at line 489 of file Polynomial.h.

template<class T>
Polynomial<T> operator- (  const Polynomial< T > &  p,
const Polynomial< T > &  q
)  [friend]
 

out-of-place polynomial substraction.

Performs the substraction $r=p-q$ .

Parameters:
[in] p a polynomial.
[in] q another polynomial.
Returns:
The result r of the operation $r=p-q$ .
See also:
operator+ (const Polynomial<T>& p, const Polynomial<T>& q)
Polynomial::operator-= (const Polynomial<T>& A)
add(Polynomial<T>& p, const Polynomial<T>& q)

Definition at line 509 of file Polynomial.h.

template<class T>
Polynomial<T> operator/ (  const Polynomial< T > &  p,
const T &  s
)  [friend]
 

out-of-place polynomial scaling.

Polynomial scaling, performs the operation $r(x)=\frac{p(x)}{s}$ .

Returns:
A constant reference to this.
See also:
mul(Polynomial<T>& r, const T& s, const Polynomial<T>& p)
Polynomial<T>::operator*= (const T& s)
operator/= (const T& s)

Definition at line 566 of file Polynomial.h.

The documentation for this class was generated from the following file:
Generated on Mon Aug 21 21:00:38 2006 for The Polynomials Templates Library by  doxygen 1.4.5