Jenkins-Traub polynomial zeros evaluator.
returns all zeros of polynomial 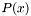
- Parameters:
-
[in] P polynomial to evaluate. T coeficients type can be either real or complex. [out] zeros vector to hold zeros. [in] polish if set to true, the zeros will be polished by Newton-Raphson algorithm on the original polynomial before deflation. This 'quick and dirty' polishing can lead to problems on large polynomials.
- Returns:
- The number of zeros found. This number can be checked against the degree of
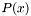 to check for errors.
to check for errors.
- See also:
- class Polynomial
newtonZero()
Definition at line 55 of file jenkinstraub.h.
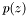
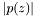 , the asolute value of
, the asolute value of 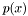 by
by 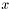 , until is has no null roots.
, until is has no null roots.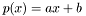
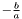
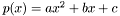 .
.![\[S=b+\sqrt{b^2-4ac}\]](form_55.png)
![\[D=b-\sqrt{b^2-4ac}\]](form_56.png)
![\[q=\left\{ \begin{array}{ll} -S & \mbox{if} \left| S\right| >\left| D\right| \\ -D & \mbox{otherwise}\end{array}\right. \]](form_57.png)
![\[z_1=\frac{2c}{q}\]](form_58.png)
![\[z_2=\frac{q}{2a}\]](form_59.png)
 1.4.5
1.4.5